√99以上 三平方の定理 解き方 260121-三平方の定理 解き方

が成り立ちます．（これを 三平方の定理 といいます．） これを用いて3辺の長さのうち2辺の長さが分かっているとき，残りの1辺の長さを求めることができます． 証明 ・・・ 証明の仕方は何十通り～何百通りあると言われています。 中でも簡単そうなb2=c2 が成り立ちます．これを「 三平方の定理 」といいます． 見かけ上「 斜めに見えている辺 」が斜辺なのではない 「 直角の向かい側 」にある辺＝「 一番長い辺 」が斜辺 例1 直角をはさむ2辺の長さが与えられると斜辺の長さが求まります． 3222三平方の定理を直接証明するというものではないので、ややこしく感じるかもしれません。 納得できない人のために、次は図で直感的に理解できるよう解説します。 三平方の定理が直感的にわかる図 三平方の定理は各辺の2乗の等式です。

三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生

三平方の定理 解き方

三平方の定理 解き方-直角三角形においては三平方の定理が成り立つため，3つの角が30°，60°，90°である直角三角形と，45°，45°，90°である直角三角形の3辺の長さには，それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

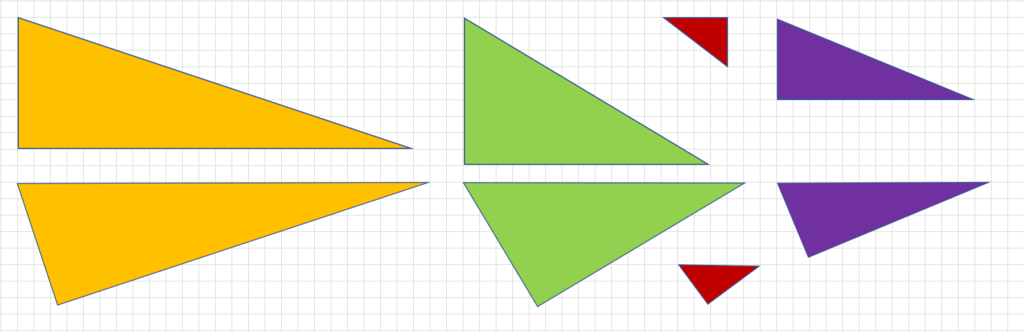
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

三平方の定理_座標平面の三角形 座標上の2点A,Bの距離 A (x1, y1),B (x2, y2)とすると 線分ABの長さ = (x 1 x 2) 2 (y 1 y 2) 2 A B x y O名前をなんとなく憶えているけどーなんだっけ？ という風に正直、自分はもうほとんど忘れていました 三平方の定理とは 直角三角形の直角を挟む2辺の長さをa, bとし、斜辺をcとすると c^2 = a^2 b^2 が成り立つことをいいます ※a^2はaの二乗下の三平方の定理の証明の方法について，太郎さんと花子さんが考えています。あとの(1)， (2)の各問いに答えなさい。 三平方の定理 直角三角形の直角をはさむ2辺の長さを a，b， 斜辺の長さをc とすると，次の関係が成り立つ。 a 2＋ b ＝ c

正三角形の高さと面積の求め方 について解説していくよ！ ここでは、中3で学習する三平方の定理という知識を利用していきます。 三平方の定理があいまいな方は、まずはこちらの記事で確認しておいてくださいね(^^) この問題も解き方はおんなじだ。 まず、真ん中の辺をyとして、yから計算すればいいんだね。 y² = 4² 7² y = √65 つぎはxを計算！ 65 = 5² x² x = 2√10 まとめ：三平方の定理（ピタゴラスの定理）を使えば直角三角形の辺の長さは大体わかる！ 三平方の定理とは、 「不思議な直角三角形」の不思議さを説明したもの です。 直角三角形は、上の図のような形をしていて、内側の 3 つの角のうち、 1 つが 90 度になっています。 90度（直角）を挟む辺の長さを b 、 c として、斜辺を a とすると、次の関係が成り立ちます。 a 2 =b 2 c 2 a 2 は「 a の二乗」といい、「 a × a ＝ a2 」と表記します。 a 2 =b 2 c 2

 三平方の定理（ピタゴラスの定理）を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理（ピタゴラスの定理）に代入してみると、 13² = 5² x² x = 12 あら不思議！ 長さがわからない直角三角形の辺を求めることができたね。三平方の定理より 172=h2 h2=264 h2=225三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れていくのが大事です。 今回、代表的な10問の問題を紹介して解説していくので、ぜひ挑戦してみてください

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理を使って線分の長さを求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方

 三平方の定理とは？ 下図1のような直角三角形ABCの3つの辺abcには、次のような式が成り立ちます。 ① （斜辺の2乗は他の2辺の2乗の和に等しい） これを三平方の定理といいます。 三平方の定理の計算方法 図1の3つの辺abcを三平方の定理を使って求めてみ三平方の定理 発展問題まとめ お疲れ様でした！ 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことが 最後三平方の定理を早く計算するテクニックを紹介します。 練習問題を用意しましたので是非この解き方をマスターして下さい。 練習問題 三平方の定理は中学・高校、さらには大学の様々な分野で使われます。

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト

1

左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) 解き方 直角三角形に対し三平方の定理を使います。 (2)は直角三角形が無いですね。 補助線を引いて直角三角形を作ります。 そのうえで高さを求めていきます。 解説 (1)次の三角形のabの長さを求めなさい。

最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ

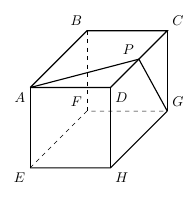
空間図形の三平方の定理の問題の解法 夢を叶える塾

 三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います3 次の立体の表面積と体積を求めなさい。 (1) 正四角錐 (2) 円錐 5㎝ 9 ㎝ 6 ㎝ 7㎝ 三平方の定理⑥ 空間 図形への利用（1） b 学 年 3 年 学習日： 月 日（ ） 中学校数学・ワークブック 中学校数学 3b7 －6b 年 組 氏名B2c2=a2 が成り立つ． 三平方の定理を使えば，直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる． たとえば次の図では， b , c が分かっていれば a が求められる． a , c が分かっていれば b が求められる． a , b が分かっていれば c が求められる． 例1 次の図で黄色の三角形について三平方の定理を使うとAHの長さが求めることができ， さらに求めたAH

三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント

中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し桃 == 《三平方の定理》 == → 印刷用PDF版は別頁 《解説》 次のような直角三角形の3辺の長さについては， a 2 b 2 =c 2 が成り立ちます．（これを 三平方の定理 といいます．） これを用いて3辺の長さのうち2辺の長さが分かっているとき，残りの1辺の長さを求めることができます． 証明 ・・・ 証明の仕方は何十通り～何百通りあると言われています。 中でも三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。

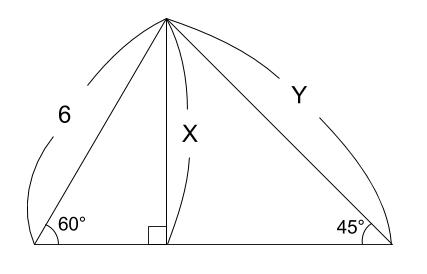
中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

Studydoctor特別な三角形と三平方の定理 中学３年数学 Studydoctor

三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。三平方の定理の逆を証明する 三平方の定理の逆って、なんで成り立つの？ 証明はどうすんの？ ってことをお話していきます。 3辺の長さが の三角形において が成り立つならば、 ABCはcを斜辺とする直角三角形となることを証明せよ。 まずは、 が三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

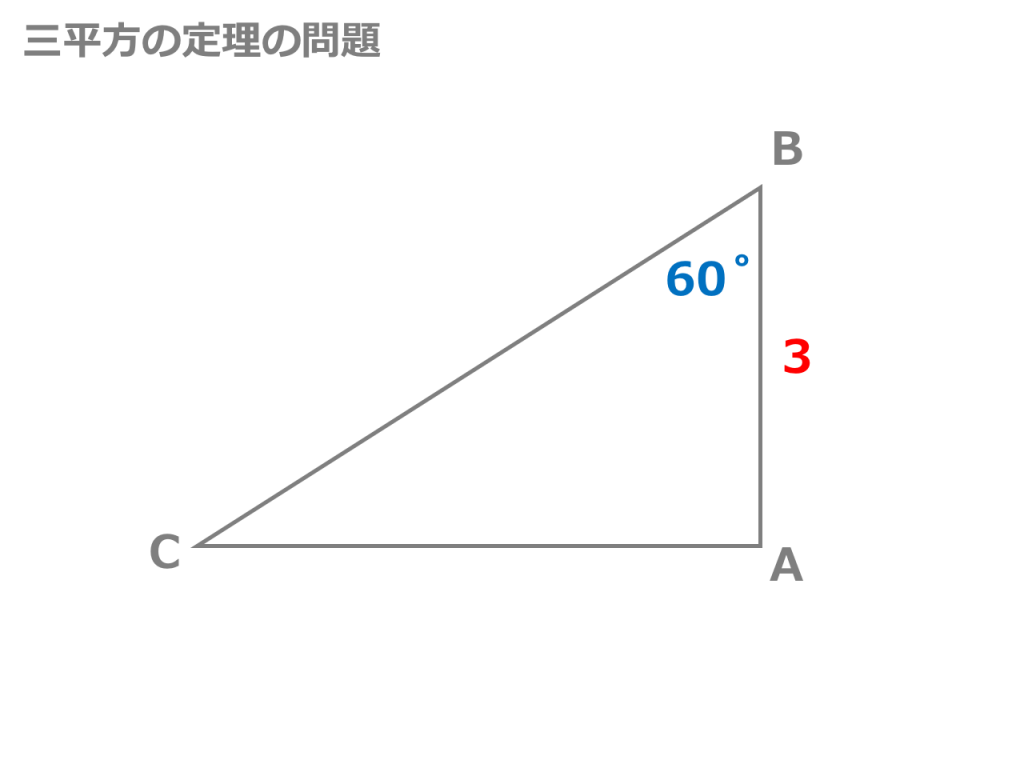
3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ

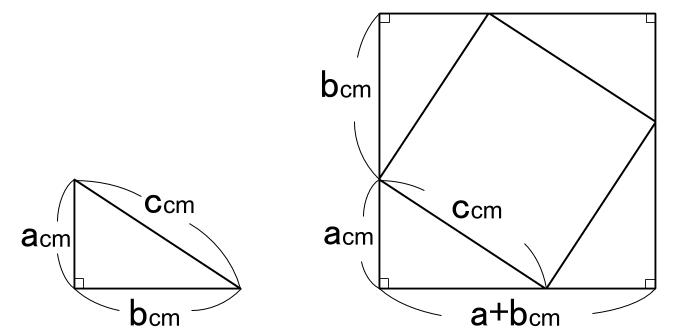
中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

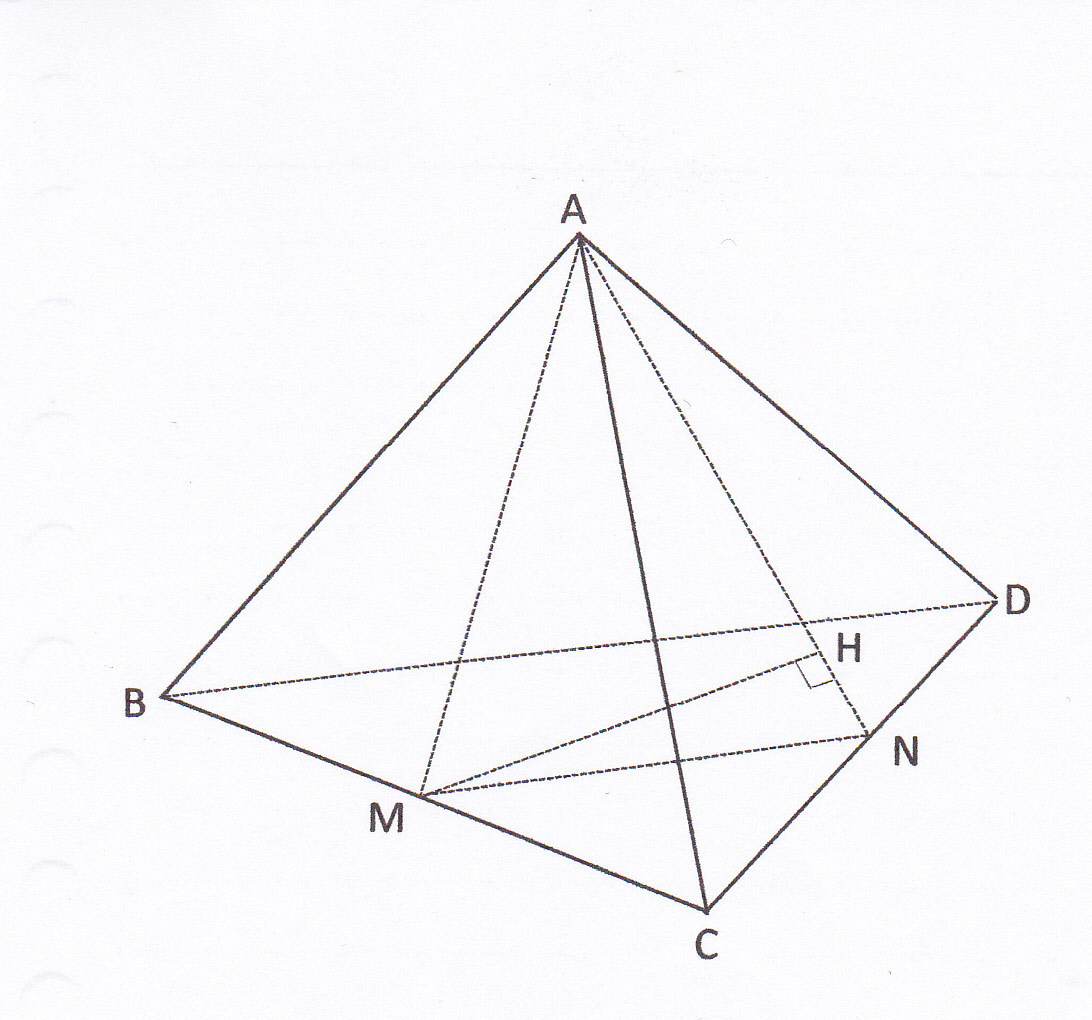
三平方の定理 中点連結定理と空間図形の融合問題の解き方 現役塾講師のわかりやすい中学数学の解き方

三平方の定理の証明と使い方

公文式の数学です 今これ三平方の定理の所なんですが 私の解答は三 Yahoo 知恵袋

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

1

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

三平方の定理のこの問題の解き方と答えを教えてください 答えが Yahoo 知恵袋

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

三平方の定理図の三角形で辺abの長さを求めよ Ac 6cmb Yahoo 知恵袋

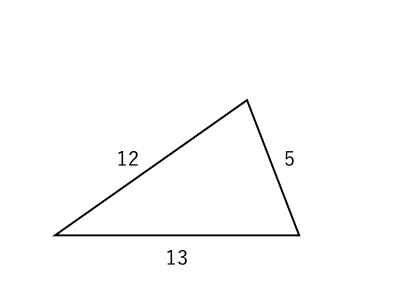
三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に

三平方の定理 ｈｏｍｅ

三平方の定理で辺を求める Youtube

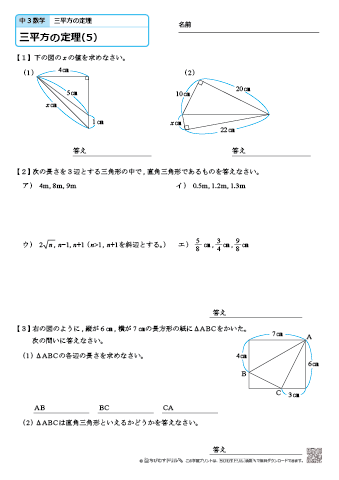
中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

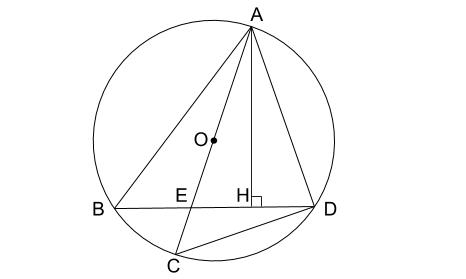
高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

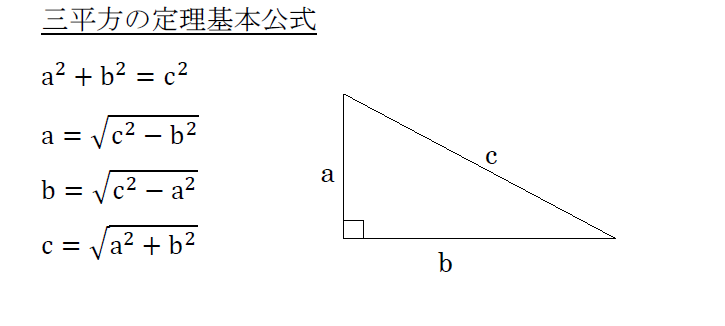
三平方の定理 覚えておきたい基本公式を解説 数スタ

なぜ 三平方の定理で角度bが90度だとわかるのですか Clear

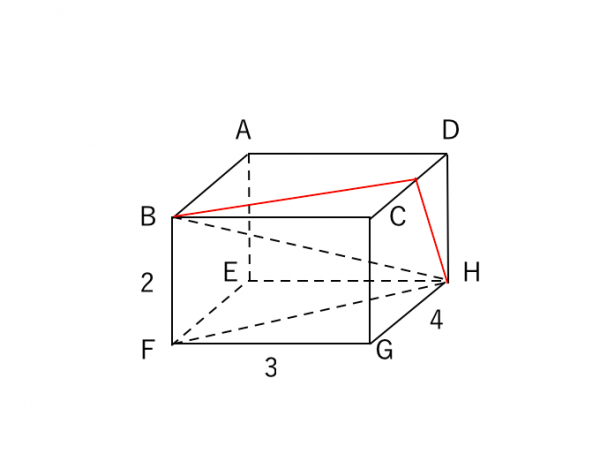
三平方の定理 立体 苦手な数学を簡単に

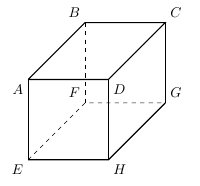
空間図形の三平方の定理の問題の解法 夢を叶える塾

三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生

三平方の定理 小学生バージョンの解き方 江戸川女子中 09年 算数解法の極意

3辺の長さが与えられたときの三角形の面積 中学 高校数学 身勝手な主張

中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット

Math 三角形に内接する円 働きアリ

三平方 折り返し

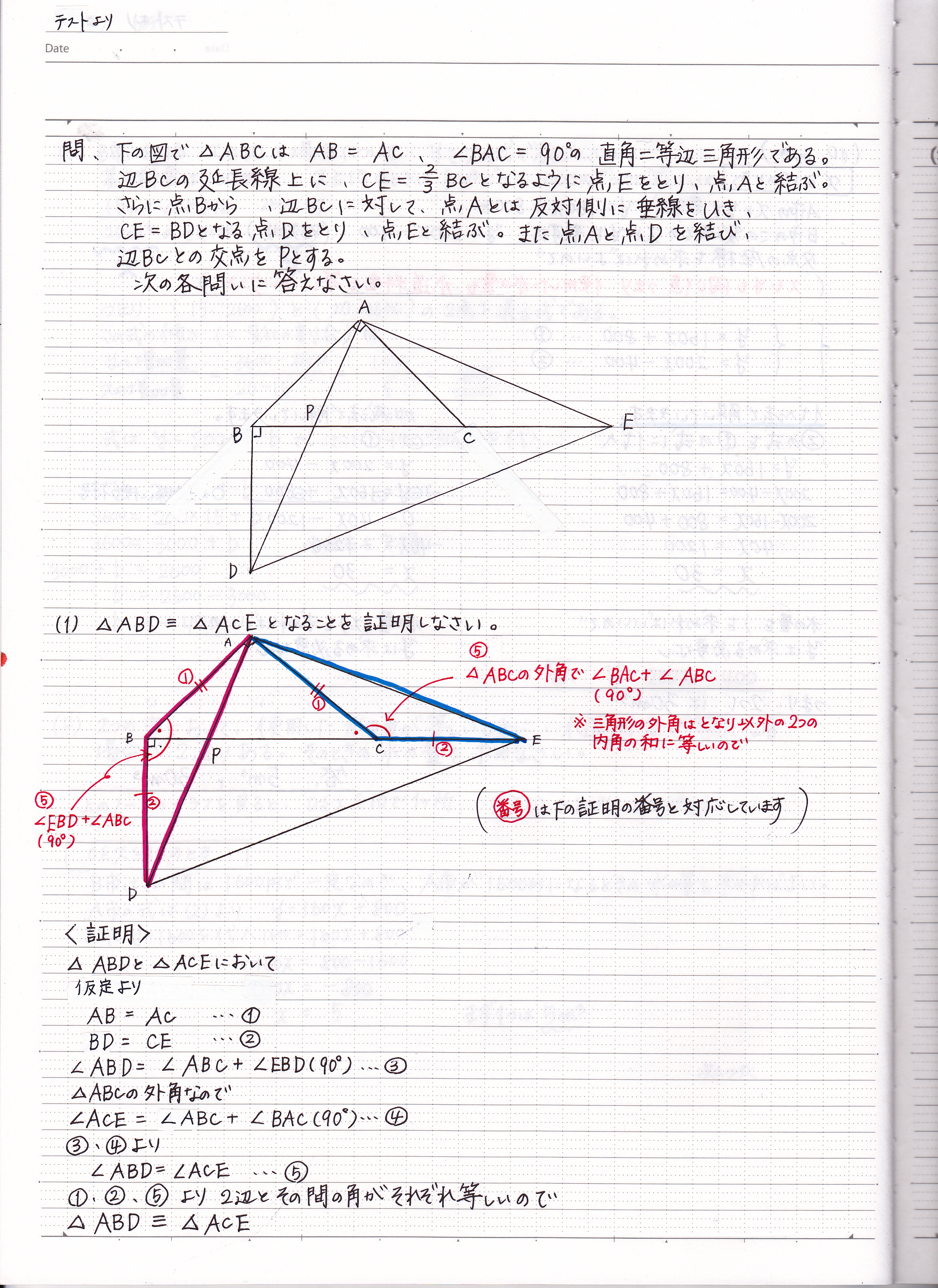
図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方

中3の三平方の定理の問題なんですが 解き方が分かりません 教えてください Clear

エコ鉄 A Twitter 汚い解き方 三平方の定理を使う 出題に即して都合よく読み替える

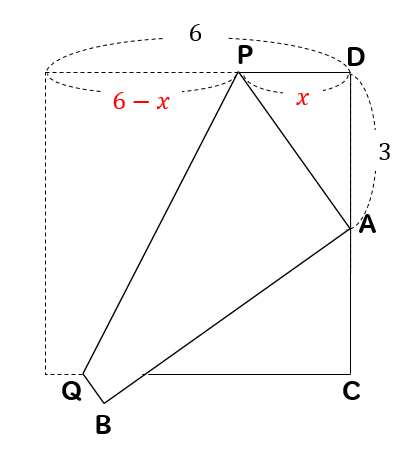
三平方の定理 方程式を利用する発展問題を解説 数スタ

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

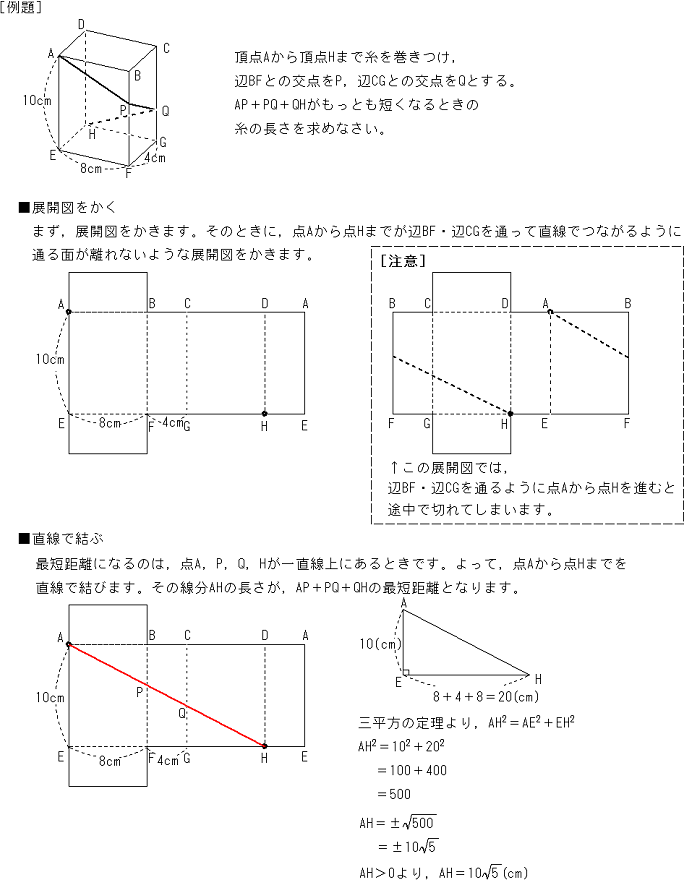
三平方の定理 立方体で最短距離を求める問題の解き方 中学数学 定期テスト対策サイト

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 証明 後編 全国入試問題解法 とんとん Youtube

数学 中3 61 三平方の定理 基本編 Youtube

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

高校数学 三平方の定理による三角関数の計算 １ 映像授業のtry It トライイット

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト

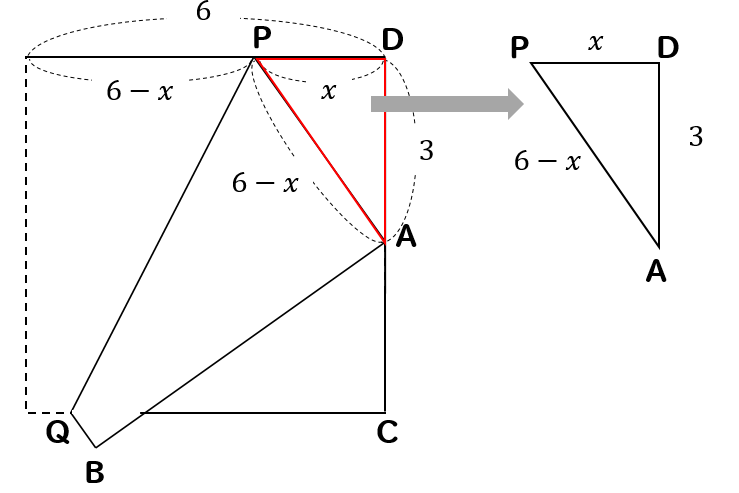
三平方の定理 方程式を利用する発展問題を解説 数スタ

三平方の定理の利用 四角錐 円錐 チーム エン

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける方解き方 Clear

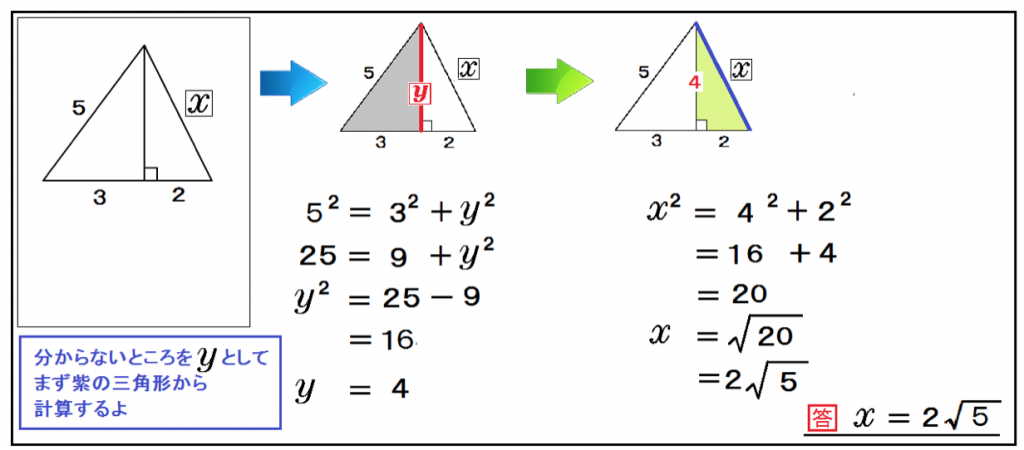
三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

Mathematics 三平方の定理 ４ 円と三平方の定理 働きアリ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学

1

正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

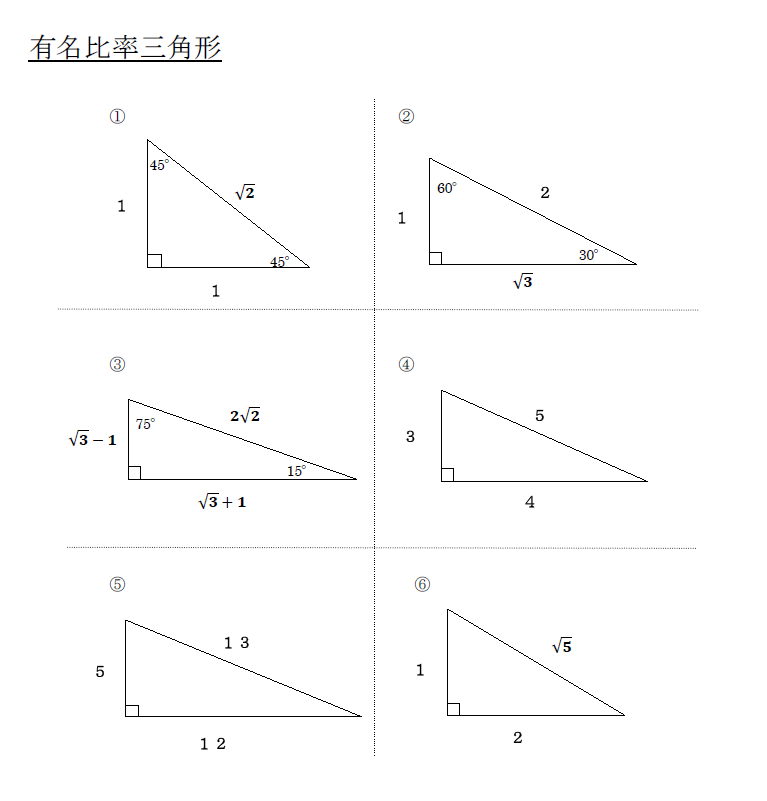
受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学

三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット

三平方の定理の証明と使い方

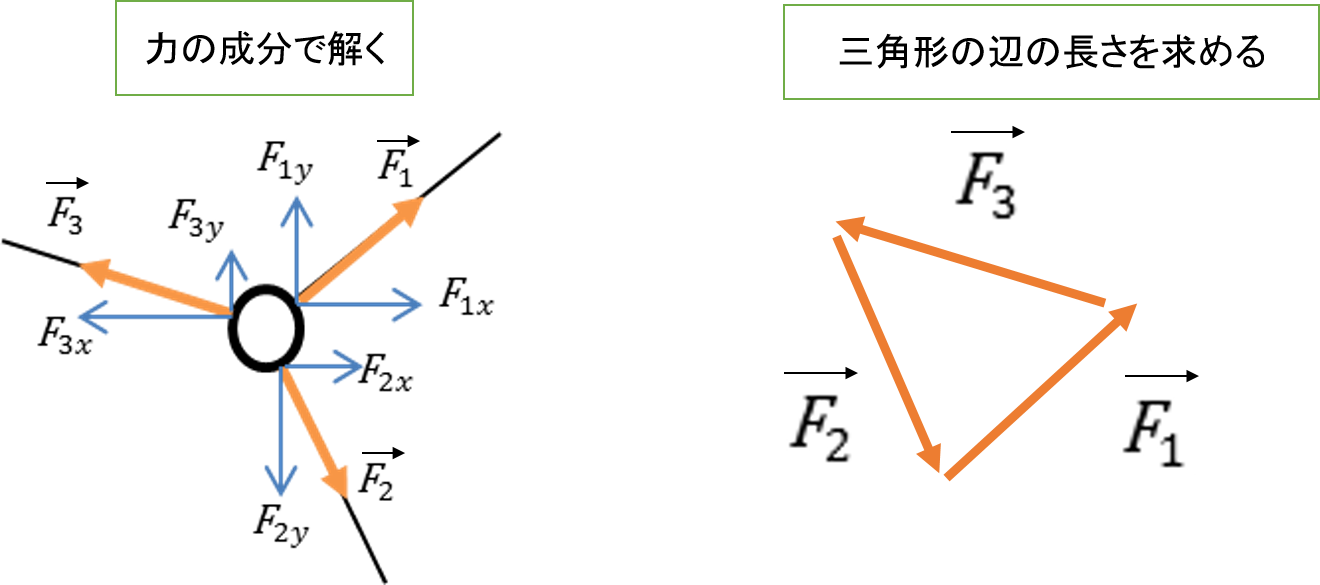
3力のつりあい 物理基礎 第二の壁 二つの解き方で乗り越えよう 平川ブログ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ

中学数学 高校入試対策dvd 見て攻略 入試の解き方 5 三平方の定理 本 通販 Amazon

受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト

1 1 ルート2 三角形

三平方の定理の応用

三平方の定理です この問題の解き方を教えていただきたいです Clear

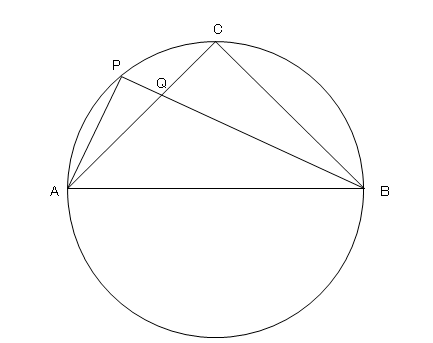
三平方の定理の応用 3 ネット塾

1

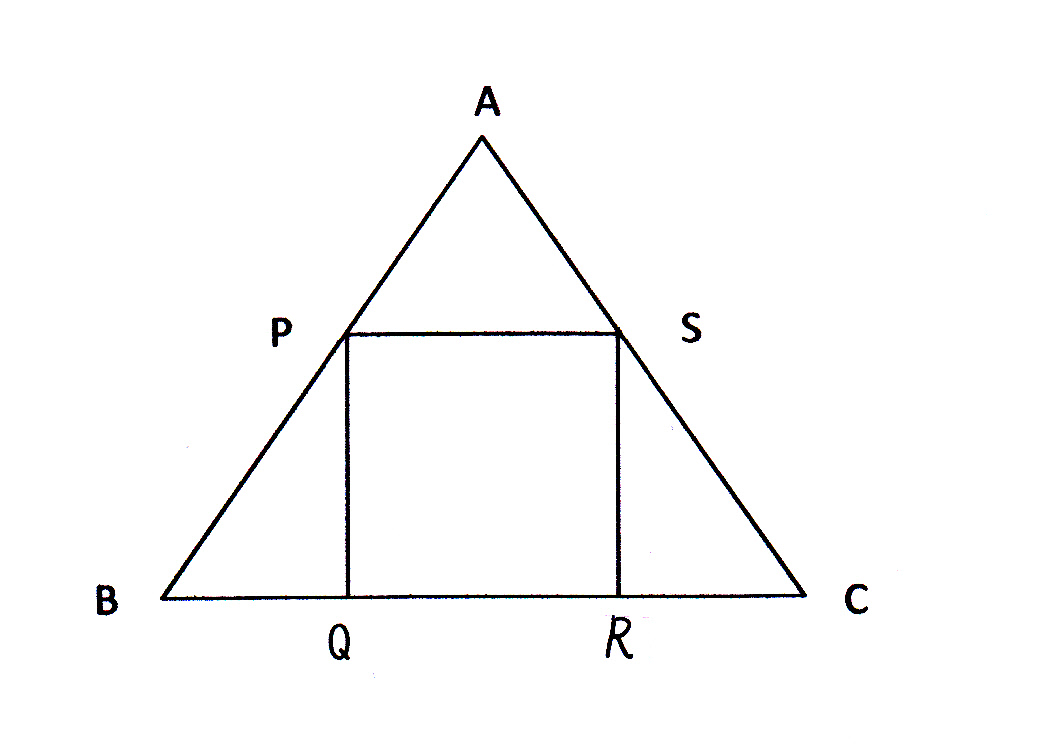
三平方の定理を使って線分の長さを求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理の証明と使い方

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

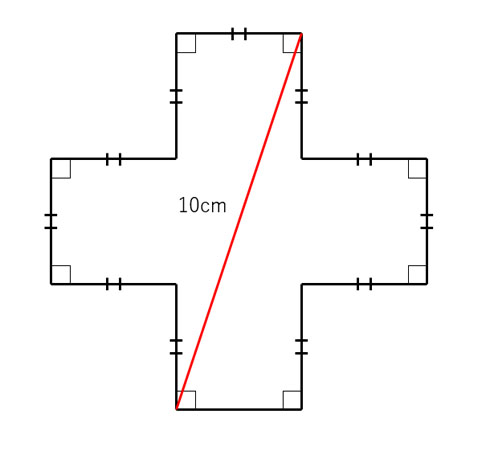
この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ

三平方の定理の練習問題10問 解き方の解説 数学fun

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

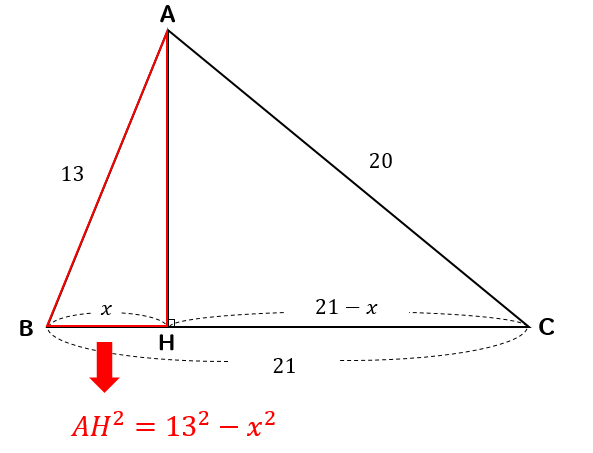
三平方の定理 方程式を利用する発展問題を解説 数スタ

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

三平方の定理でしょうか なるべく簡単な解き方教えてください 解説付 Okwave

三平方の定理の証明と使い方

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

中学数学三平方の定理についての質問です この下の問題の解き方が分かりませ Yahoo 知恵袋

三平方の定理の練習問題10問 解き方の解説 数学fun

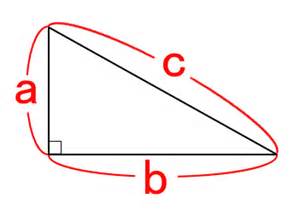
三平方の定理の楽な計算方法 完全個別指導の修優舘

都立高校入試過去問解説 相似と三平方の定理で解く平面図形問題 みみずく戦略室

Mathematics 高校入試問題研究 数学 ３ 大阪府公立高校入試 前期 理数科 平成２１年度 働きアリ The 2nd

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

Incoming Term: 三平方の定理 解き方,